
Mapa de Königsberg en la época de Leonhard Euler, famoso matemático que resolvió el problema en 1736, dando origen a la teoría de grafos
Picotazos de historia
Cómo un enigma de 1736 dio origen a los algoritmos que controlan nuestras decisiones
La resolución del problema de los siete puentes de Königsberg dio origen a la teoría de grafos gracias a la cual es posible estudiar recorridos y flujos, así como su optimización, lo que hoy resulta vital en informática
En matemáticas y ciencias, un grafo es un conjunto de objetos, denominados vértices o nodos, unidos por enlaces conocidos como aristas o arcos. Esto permite representar relaciones binarias entre elementos de un conjunto.
Pasemos ahora al año de gracia de 1736, en la ciudad de Königsberg, capital de la Prusia Oriental y uno de los más importantes centros culturales de Europa, gracias a la excelencia de su universidad y de su claustro de profesores. Por cierto, en este momento Emmanuel Kant vive en Königsberg y tiene doce años de edad.
Es durante estos años cuando la Mancomunidad Polaco-Lituana se encuentra en plena disputa —lo que se conocerá como la Guerra de Sucesión Polaca— por ver cuál de los dos principales pretendientes a la corona conseguirá triunfar: Augusto II, llamado el Fuerte porque físicamente es un titán, y Estanislao Leszczynski. Este último se establecería en Königsberg, acompañado por su corte.
Aunque en octubre del año anterior (1735) se había firmado una paz preliminar, el conflicto no finalizaría hasta la firma del Tratado de Viena, en 1738. Hasta entonces, Estanislao permanecería en la ciudad prusiana, aportando alegre mundanalidad a la severidad académica.
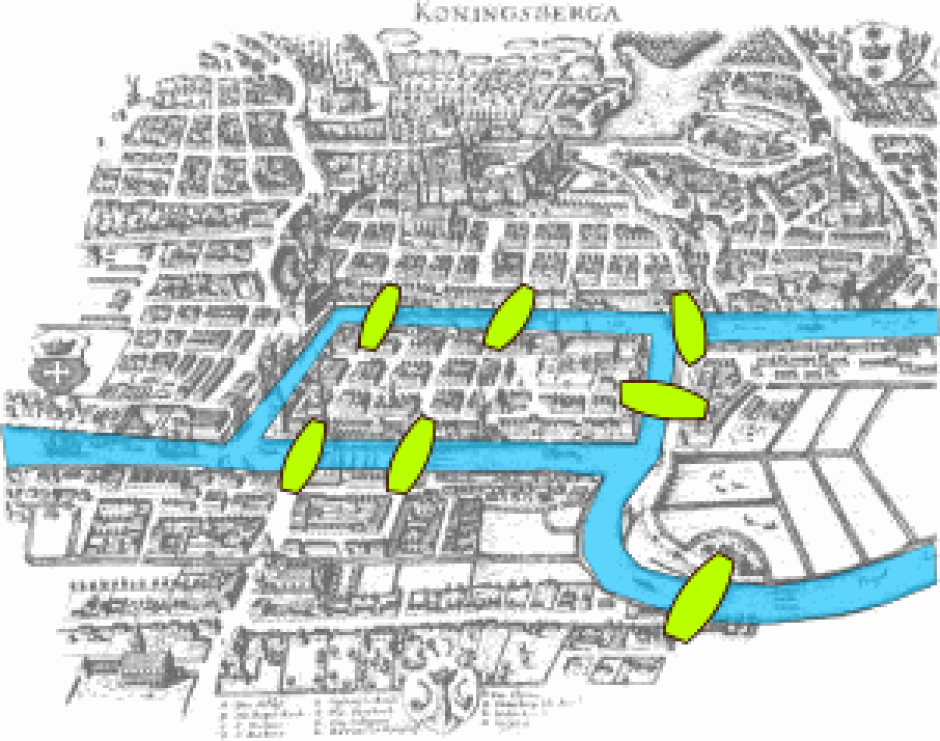
El problema de los siete puentes de Königsberg, resuelto por Leonhard Euler
La ciudad de Königsberg se asienta a ambas orillas del río Pregel o Pregolia, que la atraviesa. En el centro de la ciudad, el río tiene dos islas. La isla más pequeña se llama Kneiphof y apenas tiene diez hectáreas de extensión. La isla mayor, conocida como Lomse (hoy rebautizada como Oktyabrsky), tiene diez kilómetros cuadrados. En la época de la que hablamos —el año 1736— ambas islas estaban unidas por un puente. Kneiphof tenía cinco puentes: dos a cada lado que conectaban con cada una de las orillas del río y un quinto que la conectaba con su isla hermana. Por su parte, la isla de Lomse tenía tres puentes: uno para cada orilla del río y el tercero que la unía con Kneiphof. Estos son los famosos Siete Puentes de Königsberg.
Estos siete puentes dieron lugar a un problema conocido como el Problema de los Siete Puentes de Königsberg, que planteaba si era posible recorrer la ciudad cruzando cada uno de los puentes solo una vez.
El matemático y erudito Leonhard Euler (1707–1783) se encontraba de visita en la ciudad cuando le plantearon el ingenioso problema. Entonces, Euler era titular de la cátedra de Matemáticas en la Academia Imperial Rusa de Ciencias, en San Petersburgo. Intrigado por el enigma, se puso a meditar su solución.

Leonhard Euler, famoso matemático que resolvió el problema en 1736, dando origen a la teoría de grafos. Retrato de 1753
Pensó y dio con ella: no era posible realizar dicho recorrido. Lo demostró matemáticamente, creando lo que hoy se considera el primer teorema de la teoría de grafos. Esta teoría permite determinar relaciones entre pares ordenados (grafos). Gracias a ella, es posible estudiar recorridos y flujos, así como su optimización, lo que hoy resulta vital en informática, especialmente en los algoritmos de búsqueda y en la mejora de métodos de trabajo. Esta fue la primera demostración histórica y rigurosa sobre la teoría de las redes o grafos, sentando las bases de esta rama de la combinatoria.
Estas elucubraciones del señor Euler —que entonces se tomaron como un divertimento intelectual sin mayor trascendencia; les estoy oyendo decir: «¿Eso para qué sirve?» o «¡No da dinero!»— tienen hoy una importancia crítica, en tanto que nuestras vidas están cada vez más condicionadas por las redes sociales, profesionales, etc., y la recolección de nuestros datos, que son almacenados y analizados mediante esta teoría para determinar nuestro comportamiento y deseos. La teoría que se deriva del problema de los puentes de Königsberg es la base de los algoritmos de búsqueda de las redes, los mismos que se manipulan para influir en nuestros gustos, compras, opiniones, etc.
Por cierto, de los puentes que contempló Euler solo quedan dos. Dos no sobrevivieron a los bombardeos de la Segunda Guerra Mundial. Otros dos quedaron tan dañados que debieron ser derribados; dos más fueron destruidos y una autopista ocupó su lugar. El séptimo fue reconstruido antes de la guerra (1935), luego reparado y más tarde parcialmente reconstruido, por lo que del original queda poco.


